神经网络（Neural Network）是目前最火的机器学习算法，常见的深度神经网络有：卷积神经网络（CNN）、循环神经网络（RNN）等，在计算机视觉、语音交互、自然语言处理等领域发挥着重要作用。

那么，神经网络到底长啥样？CNN、RNN又是啥玩意儿呢？ 下面让我们一探究竟。

神经元

神经元（Neuron）是构建神经网络的最基本单元。在数学上，机器学习中的神经元就是一个数学函数的占位符（placeholder），它的工作就是对输入使用一个函数生成一个输出。

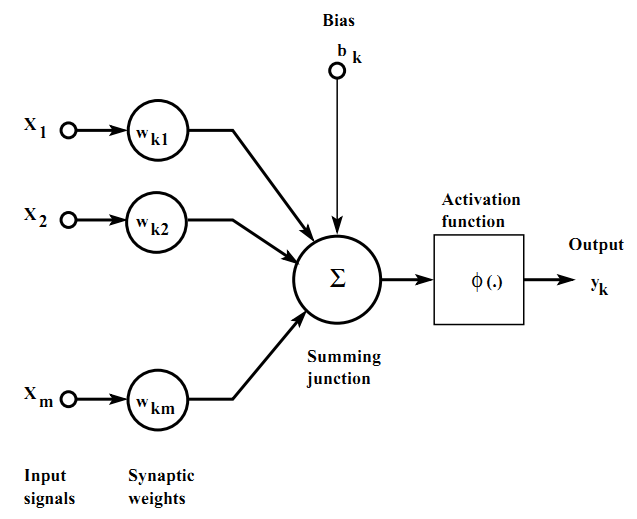
一个典型的神经元由以下三个部分组成：

• 突触集：输入信号乘上的系数，称为权重。
• 加法器：将加权后的输入进行求和。
• 激活函数：相加的结果通过激活函数之后如果大于某个值就激活这个神经元，主要的激活函数有：step, sigmoid, tanh 和 ReLU。

Step函数

数学定义如下：

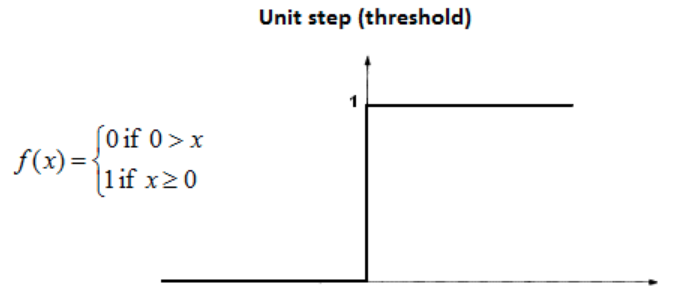
其中，如果x的值大于等于零，则输出为1；如果x的值小于零，则输出为0。我们可以看到阶跃函数在零点是不可微的。目前，神经网络采用反向传播法和梯度下降法来计算不同层的权重。由于阶跃函数在零处是不可微的，因此它并不适用于梯度下降法，并且也不能应用在更新权重的任务上。

为了解决这个问题，就引入了sigmoid函数。

Sigmoid函数

数学定义如下：

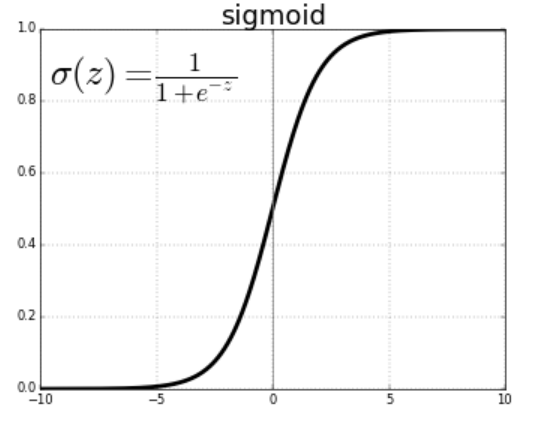
当z或自变量趋于负无穷大时，函数的值趋于零；当z趋于正无穷大时，函数的值趋于1。需要记住的是，该函数表示因变量行为的近似值，并且是一个假设。现在问题来了，为什么我们要用sigmoid函数作为近似函数之一？有以下几个原因：

• 它在可以捕获数据的非线性。虽然是一个近似的形式，但非线性的概念是模型精确的重要本质。
• Sigmoid函数在整个过程中是可微的，因此可以与梯度下降和反向传播方法一起使用，以计算不同层的权重。
• 假设因变量服从sigmoid函数相当于假设自变量服从高斯分布，也就是正态分布。许多随机发生的事件都符合正态分布。

但是，sigmoid函数存在梯度消失的问题。从图中可以看出，sigmoid函数将输入压缩到一个非常小的输出范围[0,1]，并具有非常陡峭的梯度。因此，输入空间中仍然有很大的区域，即使变化很大也只会对输出产生很小的影响。这就是梯度消失问题。这个问题随着网络层数的增加而增加，从而使神经网络的学习停滞在一定的水平上。

Tanh函数

是sigmoid函数的缩放版本，输出范围变成了[-1,1]而不是[0,1]。

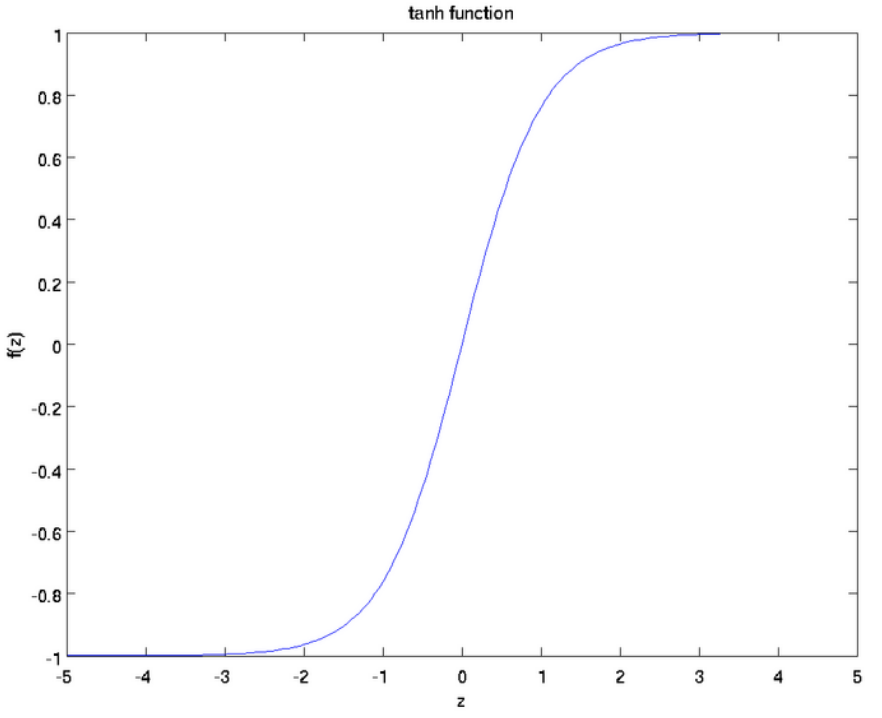
在某些地方使用tanh函数代替sigmoid函数的原因，通常是因为当数据分布在0周围时，其导数值更高。一个更高的梯度有助于提高学习速率。下图展示了两个函数tanh和sigmoid的导数值。

对于tanh函数，当输入在[-1,1]之间时，得到的导数值在[0.42,1]之间。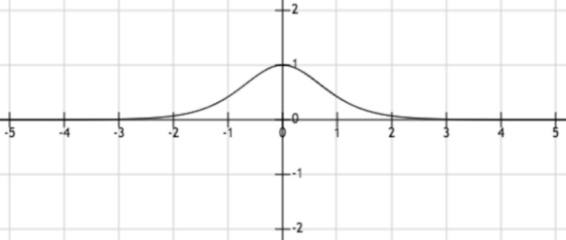

而对于sigmoid函数，当输入在[0,1]之间时，得到的导数值在[0.20,0.25]之间。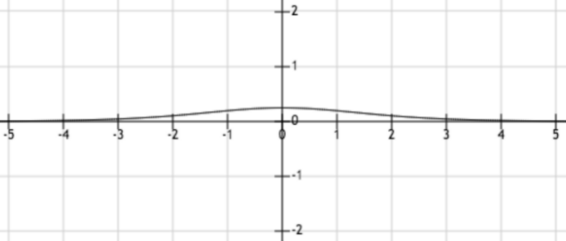

显然，tanh函数比sigmoid函数具有更大范围的导数，因此具有一个更好的学习速率。但是，在tanh函数中，梯度消失问题依然是存在。

ReLU函数

在深度学习模型中，修正线性单元（ReLU）是最常用的激活函数。
当函数输入负数时，函数输出0；输入正数时，函数输出其本身。数学表达式为f(x)=max(0, x)。

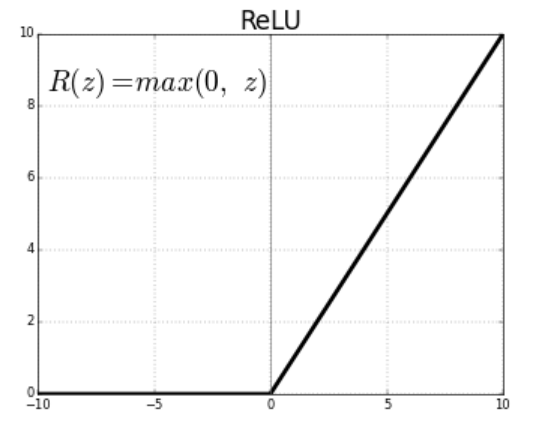
Leaky ReLU是ReLU函数最常用的一种变形，对于正数输入，其输出和ReLU一样，但是对于所有负数输入，输出不再是0，而是具有一个常数斜率（小于1）。

• 这个斜率是使用者在构建模型时设置的参数，通常称为α。数学表达式为f(x)=max(αx, x)。这样有一个优点，所有的输入x都能对输出产生影响，使得x中包含的信息被充分利用。

在实践中，ReLU通常比sigmoid和tanh函数表现更好。

神经网络

在理解一个神经网络之前，有必要去理解神经网络中的Layer(层)，一层Layer是一组有输入输出的神经元，例如，下面是一个小型神经网络。

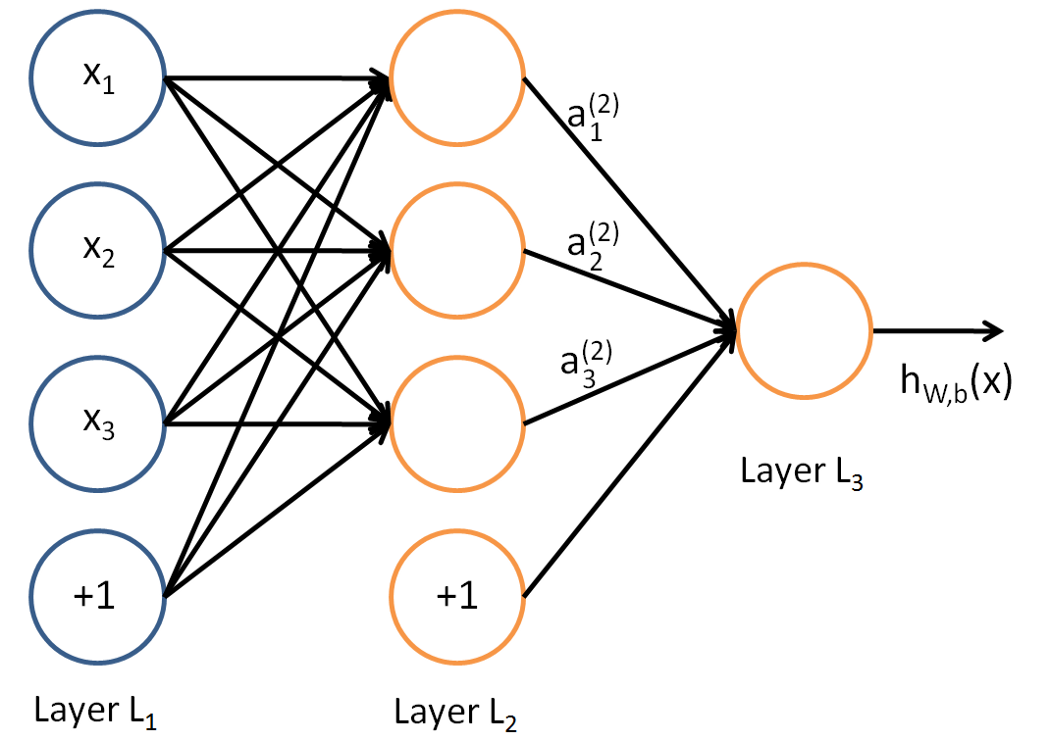
网络的最左边的layer叫做输入层，最右边的layer叫做输出层(在这个例子中，只有一个节点)。中间的layer叫做隐藏层，因为其值不能在训练集中观察到。我们也可以说，我们的神经网络例子，具有3个输入单元(不包括偏置单元)，3个隐藏单元，1个输出单元。

任何神经网络都至少包含1个输入层和1个输出层。隐藏层的数量在不同的网络中不同，取决于待解决问题的复杂度。

须注意，每一个隐藏层可以有一个不同的激活函数，例如，在同一个神经网络中，隐藏层layer1可能使用sigmoid函数，隐藏层layer2可能使用ReLU，后续的隐藏层layer3使用tanh。激活函数的选择取决于待解决的问题以及使用的数据的类型。

一个可以做精确预测的神经网络，在其中每一层的每一个神经元都学习到了确定的权重。学习权重的算法叫做反向传播。

深度神经网络

具有超过一个隐藏曾的神经网络通常叫做深度神经网络。

卷积神经网络（CNN）

卷积神经网络（Convolutional Neural Network）是神经网络的一种，在计算机视觉领域应用非常广泛。它的名字来源于组成其隐藏层的种类。CNN的隐藏层通常包含卷积层，池化层，全连接层，以及归一化层。

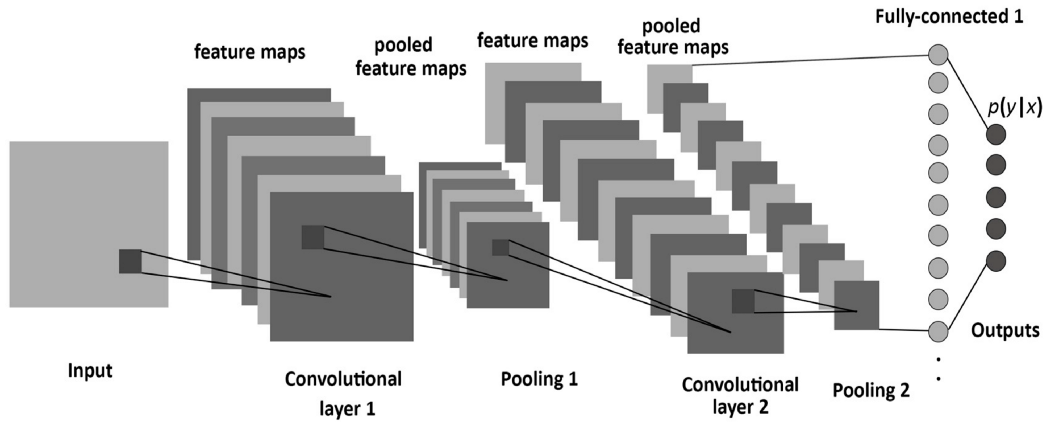
先理解两个重要概念：卷积和池化。

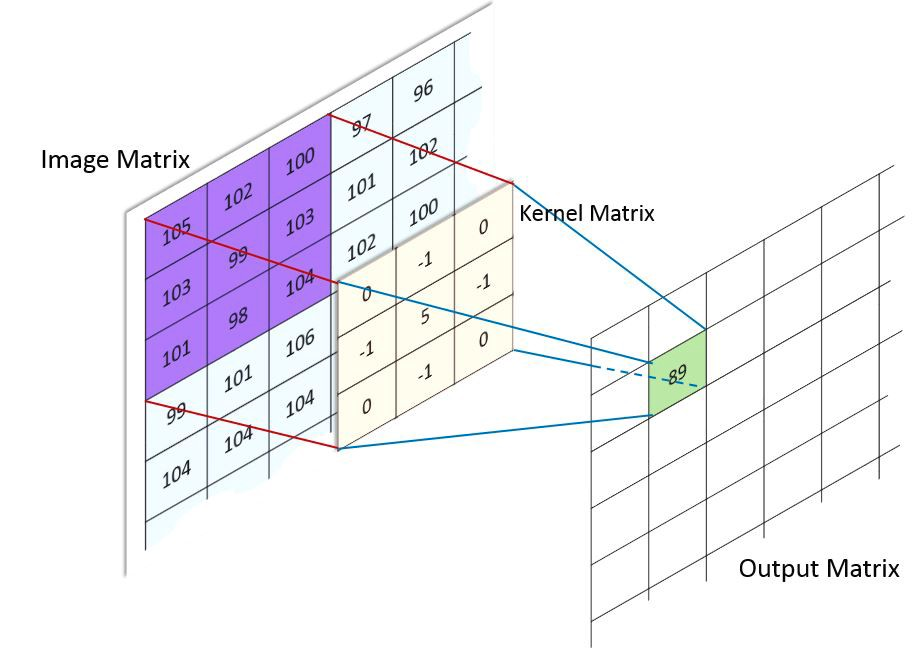
• 卷积（convolution）：用非专业的表述，就是在输入信号上使用一个“滤波器”（也叫做kernel, 核）。数学上，两个函数f和g的卷积定义如下：

$(f*g)(i)=\sum_{i=0}^m g(j)f(i-j+m/2)$

在图像处理案例中，可视化一个卷积核在整个图片上滑动是非常简单的，每个像素的值都是在这个过程中改变的。

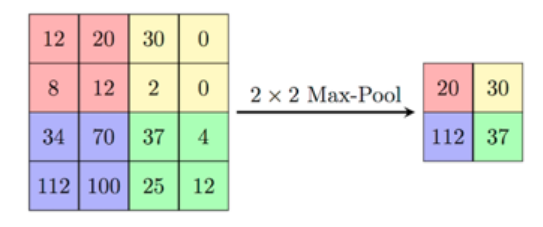
• 池化(pooling)：池化是一个基于采样的离散化处理。它的目标是对输入(图片，隐藏层，输出矩阵等)进行下采样，来减小输入的维度，并且包含局部区域的特征。

  • 有两个主要的池化种类：max和min pooling。正如其名字表明的，max pooling是在选择区域选择中最大值，min pooling是在选择区域中选择最小值。

正如我们所看到的，卷积神经网络（CNN）是一个基本的深度神经网络，它包含多个隐藏层，除之前介绍的非线性激活函数之外，这些层还使用了卷积和池化函数。

当然，简单的文字加图片可能还是很难把CNN完全讲清楚。但是，好在有一位大侠Dr. Wang开发了一个叫 CNN Explainer 的在线交互可视化工具，把CNN拆开了揉碎了，告诉我们CNN究竟是怎么一回事，为什么能辨别物品。Don`t say so much, respect：https://poloclub.github.io/cnn-explainer/

循环神经网络（RNN）

循环神经网络（Recurrent Neural Network），正如其名，是一个非常重要的神经网络种类，在自然语言处理领域应用非常广泛。在一个普通的神经网络中，一个输入通过很多层的处理后，得到一个输出，假设了两个连续的输入是互相独立不相关的。

然而这个假设在许多生活情节中并不成立。例如，如果一个人相应预测一个给定时间的股票的价格，或者相应预测一个句子中的下一个单词，考虑与之前观测信息的依赖是有必要的。

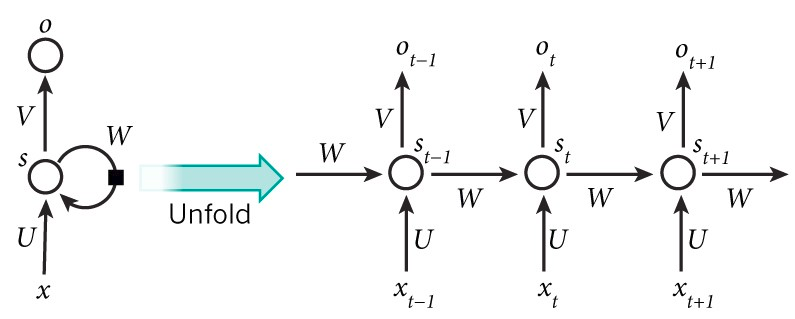
RNNs被叫做循环，因为它们对于一个序列中的每一个元素执行相同的任务，它们的输出依赖于之前的计算。另一个理解RNN的角度是，认为它们有“记忆”，能够捕捉到到目前为止的计算信息。理论上，RNN能够充分利用任意长序列中的信息，但是实践上，它们被限制在可以回顾仅仅一些步骤。

结构展示，一个RNN如下图所示。它可以想象成一个多层神经网络，每一层代表每一个确定时刻t的观测。

RNN在自然语言处理上展现了非常巨大的成功，尤其是它们的变种LSTM（Long Short Term Memory networks），它可以比RNN回顾得更多，详情请参考：
Understanding LSTM Networks

---

参考

1. 神经网络简介
2. Understanding Neutral Networks